CS3402-Lecture-4-Normal Forms
CS3402-Lecture-4-Normal Forms
函数依赖(Functional Dependency)
函數依賴是一個在數據庫中兩個屬性集合的約束
Formal definition:
- Let R be a relation schema, and α subset of R, β subset of R. We say

- If in any relation instance r(R), for all pairs of tuples t1 and t2 in r, we have:
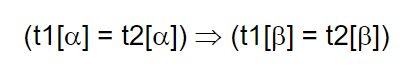
- Let R be a relation schema, and α subset of R, β subset of R. We say
Inference Rules for FDs

Closure of a set of attributes X with respect to F is the set X+ of all attribute that are functionally determined by X
- Note both X and X+ are a set of attribute
If X+ consists of all attributes of R, X is a superkey for R
- From the value of X, we can determin the values the whole tuple
X+ can be calculated by repeatedly applying IR1, IR2, IR3 using the FDs in F
From X to find out X+
Closure of a set F of FDs is the set F+ of all FDs that can be inferred from F
Two sets of FDs F and G are qeuivalent if:
- Every FD in F can be inferred from G and
- Every FD in G can be inferred from F
- Hence, F and G are equibalent if F+ = G+
Relational Database Design
Logical/Conceptual DB Design
- Schema
- what realtions are needed?
- waht their attributes should be?
- Schema
What is a “bad” DB Design?
- Repetition of data/information
- Potential inconsisitency
- Inability to represent certain information
- Loss of data/information
Introduction
- Normalization theory
- based on functional dependencies
- universe of realtions
- 1st Normal Form(1NF)
- 2NF
- 3NF
- BCNF
- 4NF
- …
- based on functional dependencies
Normalization
- Proposed by Codd(1972)
- take a relation schema through a series of tests based on FD and primary keys to certify whether it satisfies a certain normal form
- Decompose a relation into several related relation to achieve
- Minimizing redundancy
- Minimizing the insertion, deletion and update anomailes
Requires
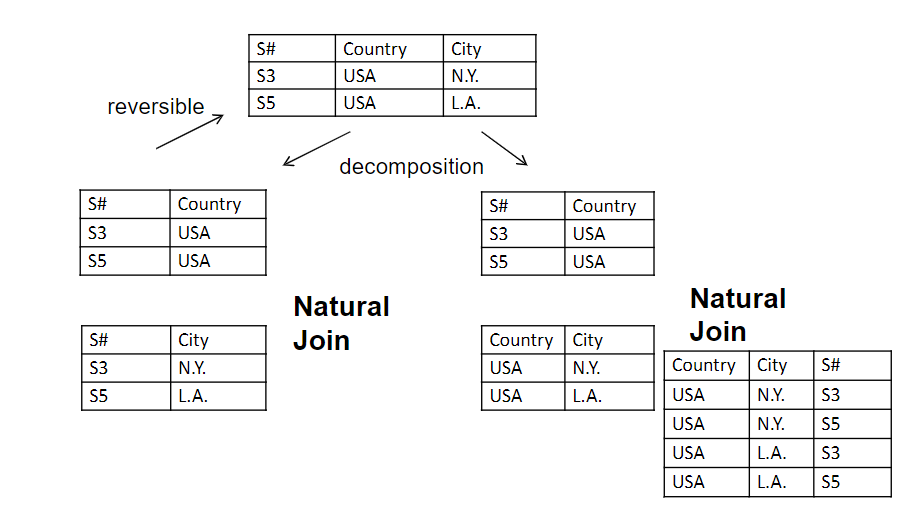
- Non-additive or lossless join
- Decomposition is reversible and no information is lost
- No spurious tuples should be generated by doing a natrural-join of any relations
- Preservation of the functional dependencies
- Ensure each functional dependency is represented in some individual relation or could be inferred from other dependencies after decomposition.
Lossless Decompositon
First Normal Form with Primary Key
First normal form(1NF)
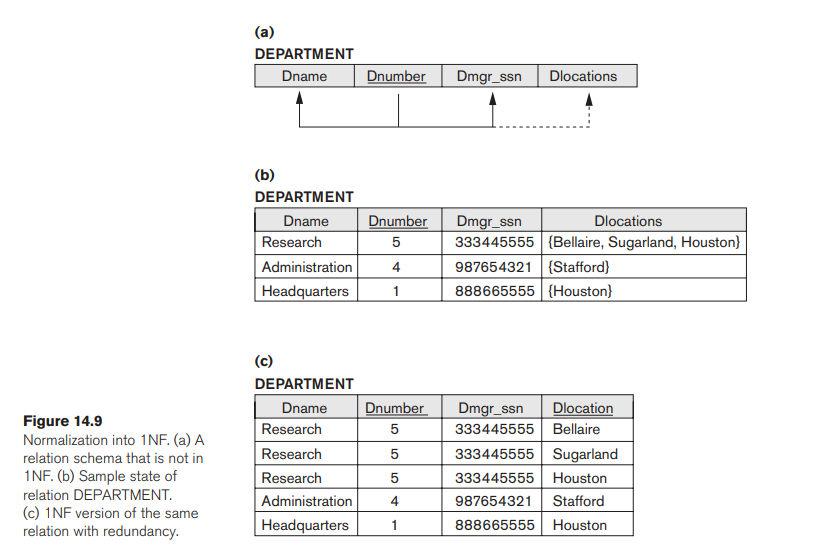
Disallow multi-values attributes, composite attributes and their combination
The domain of an attribute must be atomic value
DEPARTMENT: each department can have a number of locations
1NF: DEPT_LOCATIONS(Dnumber, Dlocation)
1NF also disallow multivalued attributes that are themselves composite

Example
FIRST(S#, Country, City, P#, Qty)and its Functional Dependency Diagram:- Whats the primary key?
(S#, P#)
Problem
Insert Anomailes
- Inailtity to represent certain information:
- E.g. cannot enter “Suppiler and City” information until Suppiler suppiles at least one product
Delete Anomailes
- Deleting the “only tuple” for a supplier will destroy all the information about that supplier
Update Anomailes
"S# and City"could be redundantly represented for eachP#. which may cause potential inconsistency when updating a tuple
Solution: 1NF->2NF
- Replace the original tabel by two sub-tables
SECOND(S#, City, County)SP(S#,P#,Qty)- and now, their FD diagrams are:
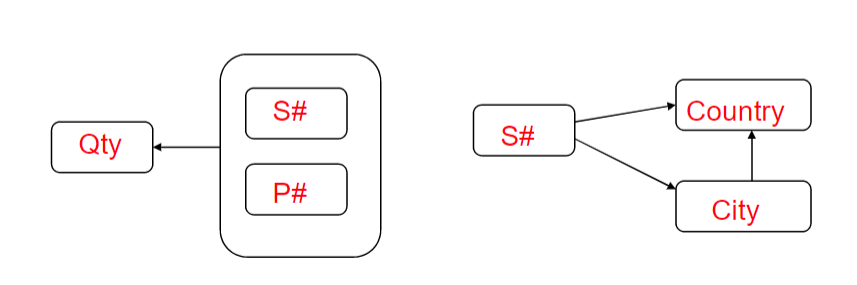
Second Normal Form with Priary Key
X -> Y
Full functional dependency
- If removal of any attribute A from X means that the dependency does not hold any more
- E.g.
{S,P} -> Qty
Partial functional dependency
- If some attributes A belonging to X can be removed from X and dependency still holds
- E.g.
{S,P}->Country as S#->Country
A realtion R is in 2NF if every nonprime attributes A in R is fully functinal dependent on the primary key of R
An attribute of R is called prime (key) attribute of R if it is a member of some candidate key of R. Otherwise it it nonprime.
Non-prime(non-key) attributes: Coutry, City, Qty
Primary key:
{S, P}The nonprime attributes Country violates 2NF because of
S#-> CountrySimilarly,
S#->CityIf a realtion is not in 2NF, it can be 2NF normalized into a number of 2NF relations in which nonprime attribute are associated only with the part of the primary key on which they are fully functional dependent.
Solutions:
SP(P#,S#, Qty);Second(S#, City,Country)
Problem

Insert Anomalies
- Cannot insert “City and Country” information until some Supplier in that city exist
Delete Anomalies
- Deleting an “only tuple” for a particular city will destroy all the information about that city
Update Anomalies
- The supplier move to another city, inconsistency between city and country will happen
Solution: 2NF->3NF
- Replace the SCOND table by two sub-tables
SC(S#,City)
CC(City, Country) - and still keep the table
SP(S#,P#,Qty). Now the FD diagram for the new tables: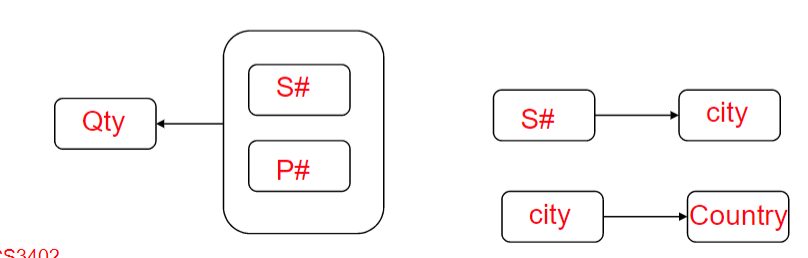
Third Nomal Form with Primary Key
3NF is based on the concept of transitive dependency
A functional dependency X->Y in a relation R is transitive dependency if there exists a set of attributes Z in R that is neither a candidate key nor a subset of any key of R, and both X->Z and Z->Y hold
X->Z->Y
E.g., dependency
S#->Countryis transitive through CityS#->Cityand City->Country, and City is neither a key itself nor a subset of the keyS#->City->Country
According to Codd’s original definition, a relation scheme R is in 3NF if it satifies 2NF and no non-prime attribute of R is transitively dependent on the primary key
To normalize R into 3NF, R should be decomposed to break the transitive dependency.
3NF:
SC(S#,City),CC(City,Country),SP(S#,P#,Qty)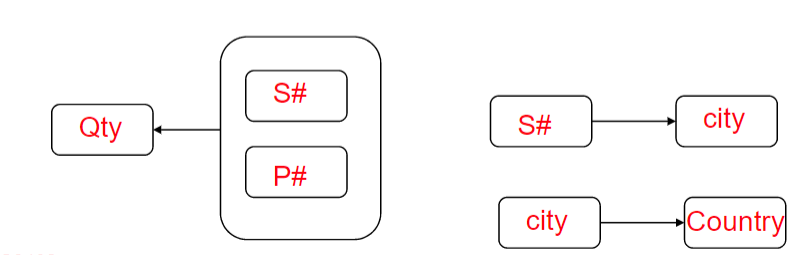
Normal Form Defined Informally
1st normal form
- All attributes are simple
2nd normal form
- All non-prime attributes depend on the whole key
3rd normal form
- All non-prime attributes only depend on the key
In general, 3NF is desirable and powerful engough
But, still tere are cases where a stronger normal form is needed

General Definitions of 2NF and 3NF
Definition: A relation schema R is in second normal form(2NF) if every non-prime attribute A in R is not partially dependent on any key of R.
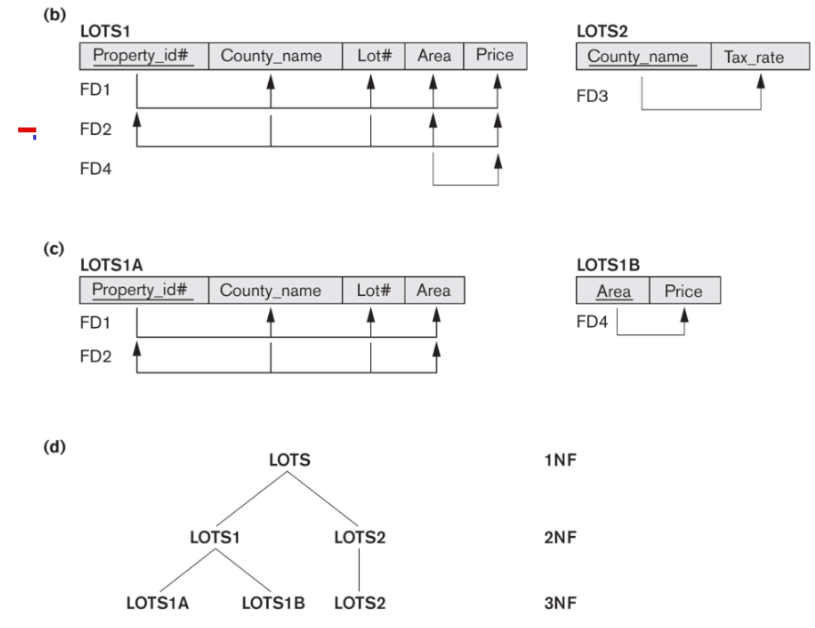
LOTS(Property_id#, Country_name)- Two candidate keys:
Property_id#andCounty_name, Lot# Property_id#is the primary key- LOTS violates 2NF due to FD3 as Tax_rate is partially dependent on the candidate key
County_name, Lot# - County_name => Tax-rate (partial dependent)
General Definition of Second Normal Form

General Definition of Third Normal Form
Definition: A relation schema R is in third normal form(3NF) if, whenever a nontrivial functional dependency X -> A holds in R, either (a) X is a superkey of R, or (b) A is a prime attribute of R
- Superkey => include a key
- Prime attributes => attributes in a key
- LOTS2 is in 3NF
- FD4 in LOTS1 violates 3NF because Area is not a superkey and
Price is not a prime attribute in LOTS1
- LOTS1 violates 3NF because Price is transitively dependent on
each of the candidate keys of LOTS via the nonprime attribute Area - To normalize LOTS1 into 3NF,
LOTS1B{Area, Price}
Boyce-Codd Normal Form
BCNF was proposed as a simpler form of 3NF, but it was found to be stricter than 3NF
Every relation in BCNF is also in 3NF
- BUT Relation in 3NF is not necessarily in BCNF
Definition: A relation schema R is in BCNF if whenever a nontrivial functional dependency X -> A holds in R, then X is a superkey of R
Difference:
- Condition which allows A to be prime is absent from BCNF