CS3103-Lecture-6
DeadLock
The Deadlock Problem
- Deadlock: a set of blocked processes each holding a resource and waiting to acquire a resource held by another process
- Example:
- a system has 2 disk drives, P1 and P2 each hold one disk drive and each needs another one
- semaphores A and B, initialized to 1
System Model
- Resources: R1, R2, …, Rm
- each represents a different resource type
- e.g. share data structure, memory space, I/O devices
- each resource type Ri has Wi instances
- each represents a different resource type
- Each process utilizes a resource in the following pattern
- request
- use
- release
Deadlock program example
- Two mutex locks are created and initialized
- Deadlock is possible if
- Thread 1 requests first_mutex and thread 2 requests second_mutex
- Thread 1 then waits for second_mutex and thread 2 waits for first_mutex
- illustrated by a resource allocation graph
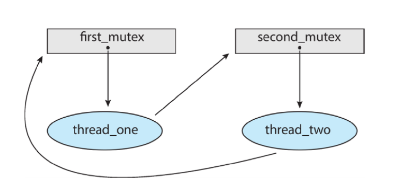
- Thread 1 requests first_mutex and thread 2 requests second_mutex
- Deadlock is possible if
Why Do Deadlock Occur?
Reason 1:
- In large code bases, complex dependencies arise between components
Reason 2:
- Due to the nature of encapsulation
- Hide details of implementations and make software easier to build in a modular way
- Such modularity does not mesh will with locking
- Due to the nature of encapsulation
Necessary Conditions of Deadlock
- Mutual exclusion: only one process at a time can use a resource
- Hold and wait: a process holding at least one resource is waiting to acquire additional resources held by other processes
- No resource preemption: a resource can be released only voluntarily by the porcess holding it, after it has completed its task
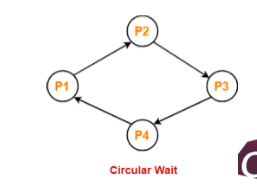
- Circular wait: there exists a set of waiting processes
p0,p1,...,pn- P0 is waiting for a resource that is held by P1
- P1 is waiting for a resource that is held by P2
- Pn-1 is waiting for a resource that is held by Pn
- Pn is waiting for a resoucrce that is held by P0
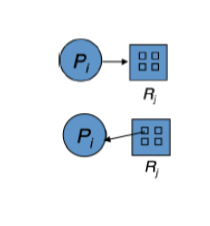
Resource-Allocation Graph
Two types of nodes:
P = P1,P2,...,Pn, the set of all the processes in the systemR = R1,R2,...,Rn, the set of all resource types in the systemTwo types of edges:
request edge: directed dege Pi -> Rj
assignment edge: directed edge Rj -> Pi
- Example:
- 1 instance of R1
- 2 instances of R2
- 1 instance of R3
- 3 instances of R4
- P1 holds an instance of R2 and is waiting for an instance of R1
- P2 holds an instacne of R1, an instance of R2, and is waiting for an instance of R3
- P3 is holds an instance of R3
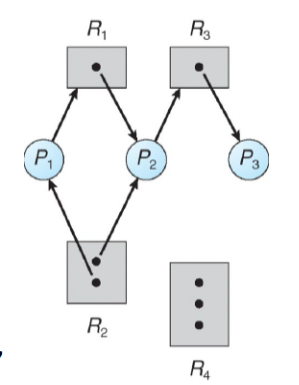
Is there a deadlock?
- No
- But will be deadlock if P3 starts to wait for R2
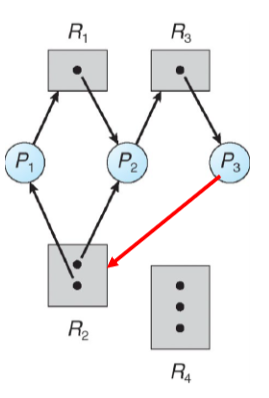
Is there a deadlock?
- circular wait does not necessaryly lead to deadlock
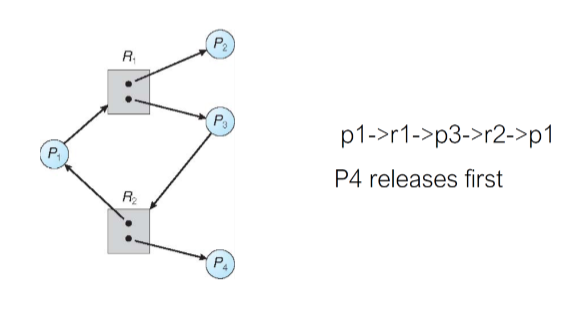
- circular wait does not necessaryly lead to deadlock
Facts
- If graph contains no cycle -> no deadlock
- If graph contains a cycle
- if only one instance per resource type -> deadlock
- If several instance per resource type -> possibility of deadlock
How to Handle Deadlocks
Ensure that the system will never enter a deadlock state
- Prevention: ensures that at least one of the necessary condtions to cause a deadlock will never occur
- Avoidance: ensures that the system will not enter an unsafe state
Allow the system to enter a deadlock deadlock state and then recover
- Deadlock detection and recovery: detect the existence of deadlock and recovery to a safe state
Deadlock Prevention - Hold-and-wait
- Provide a total ordering on lock acquisition
- This approach requires careful design of global locking strategies
- Example
- There are two locks in the system (L1 and L2)
- We can prevent deadlock by always acquiring L1 before L2

Process can request a resource only if not hold other resources
- require process to request all its resources before it begins execution; allow process to request resources only when the process has non
low resource tilization
possible starvation
Acquire all locks at once, atomically
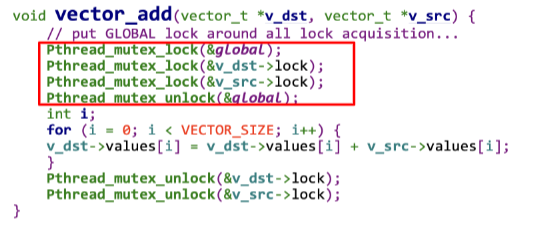
no thread switch can occur in the midst of lock acquisition
Problem:
- Require us know exactly which locks to acquire in prior
- Decrease concurrency
Deadlock Prevention - No Preemption
- Multiple lock acquisition often gets us into trouble because when waiting for one lock we are hloding another
- trylock()
- Used to build a deadlock-free, ordering-robust lock acquistion protocol
- Grab the lock (if it is available)
- Or, return -1: you should try again later

- Problem: livelock
- Both sysytems are running through the code sequence over and over again
- Progress is not being made

- Solution:
- Add a random delay before looping back and trying the entrie thing over again
Prevention - Mutual Exclusion
wait-free
- Using powerful atomic hardware instruction.
- You can build data structures in a manner that does not require explicit locking.

We now wanted to atomically increment a value by a certain amount:

- Repeatedly tries to update the value to the new amount and uses the compare-and-swap to do so
- No lock is acquired
- No deadlock can arise

Deadlock Aboidance
Dead voidance: require extra information about how resources are to be requested
- Each process declares a max number of resources it may need
Deadlock-avoidance algorithm ensure there can never be a circular-wait condtion
Resource-allocation state:
- the number of available and allocated resources
- the maximum demands of the processes
Safe State
When a process requests an available resource, system must decide if immediate allocation leaves the system in a safe state
- there exists a sequence
<P1, P2,..., Pn>of all processes in the system - for each Pi, resources that Pi may still request can be satisfied by currently available resources + resources held by all the Pj, with j < i
- there exists a sequence
Safe state can guarantee no deadlock
- if Pi’s resource needs are not immediately available:
- wait until all Pj have finished(j< i)
- when all Pj (j < i ) has finished, Pi can obtain needed resources
- wait until all Pj have finished(j< i)
- if Pi’s resource needs are not immediately available:
System in safe state –> no deadlocks
SYstem in unsafe state –> possibility of deadlock
Deadlock avoidance: ensure a system never enters an unsafe state
Deadlock Avoidance Algorithms
- Single instance of a resource type: resource-allocation graph
- Multiple instances of a resource type: banker’s algorithm
Resource-Allocation Graph
Two tpyes of nodes:
P = {P1, P2, ..., Pn}, the set of all the processes in the systemR = {R1, R2, ..., Rm}, the set of all the resource types in the system
Two types of edges:
- request edge: directed dege Pi -> Rj
- assignment dege: directed edge Rj -> Pi
- claim edge: directed dege Pi -> Rj
- process Pi may request resource Rj
- dash line
Single-instance Deadlock Avoidance
Using reource- allocation graph
Transitions in between deges
- claim dge -> request edge when a process requests resource
- request dege -> assignment edge when resource allocated to process
- assignment dege -> claim dege when resource released by process

THe request can be granted only if converting a request edge to an assignemnt dege does not result in a cycle
- no cycle -> safe state
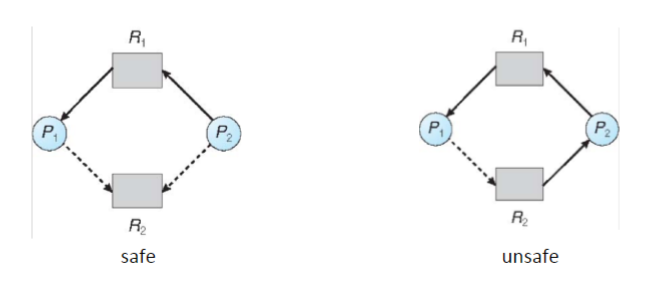
- no cycle -> safe state
Banker’s Algorithm
For multiplep-instance resource deadlock avoidance
Assumptions:
- each process must a priori claim maximum use of each resource type
- when a process requests a resource, it may have to wait
- when a process gets all its resources it must release them in a finite amount of time
Banker’s Algorithm: State Data Structure
- n processes, m type of resources
- available: an array of length m, instance if avaiabel resource
available[j] = k:k instances of resource type Rj available
- max: a n $\times$ m matrix
max[i,j] = k:process Pi may request at most k instances of resource Rj
- allocation: n × m matrix
allocation[i,j] = k:Pi is currently allocated k instances of R
need: n × m matrixneed[i,j] = k:Pi may need k more instances of Rj to complete its taskneed[i,j] = max[i,j] –allocation [i,j]
- available: an array of length m, instance if avaiabel resource
Banker’s Algorithm: Safe State
- Data structure to compute wether the system is in a safe state
- use
work[j]to track allocatable resources of type Rj- unallocated + released by finished processes
- use
finish[i]to track whether process Pi is finished - initialize:
work[j]=available[j]for all j,finish[i] = falsefor all i
- use
- Algorithm:
- find an i satisfying
finish[i] = false && need[i,j] < work[j];if ont exist, go to step3 - with the above found i do
work[j] = work[j] + allocation[i,j] for all j, finish[i] = true, go to step 1 - if
finish[i] == true, then the system is in a safe state
- find an i satisfying
Banker’s Algorithm: Resource Allocation
Data structure: request for each process Pi and resource type Rj
request[i,j] = k-> porcess Pi wants k instances of resource type Rj
Algorithm(assuming allocating resource for Pi)
- if $\forall$ j:
request[i,j] <= need[i,j], go to 2; otherwise, raise error (exceed maximum claim) - if $\forall$ j:
request[i,j] < available[j]go to 3; otherwise Pi must wait - pretend to allocated requested resources to Pi by modifying the states
available[j] = available[j] - request[i,j] for all jallocation[i,j] = allocation[i,j] - request[i,j] for all jneed[i,j] = need[i,j] - request[i,j] for all j
- use previous algorithm to tst if ti is a safe state
- if yes -> allocate the resources to Pi
- if no -> Pi must wait, and the old resource-allocation state is restored
- if $\forall$ j:
Banker’s Algorithm: Example
System state:
- 5 processes P0 through P4
- 3 resource types: A (10 instances), B (5 instances) and C (7 instances)
Snapshot at time T0:

Why < P1, P3, P4, P2, P0> is in safe state?

- needed[1] <= work –> work = work + allocation = [5 3 2], finish[1] = true
- needed[3] <= work –> work = work + allocation = [7 4 3], finish[3] = true
- needed[4] <= work –> work = work + allocation = [7 4 5], finish[4] = true
- needed[2] <= work –> work = work + allocation = [10 4 7], finish[2] = true
- needed[0] <= work –> work = work + allocation = [10 5 7], finish[0] = true
- P1 requests 1 0 2, still in safe state?
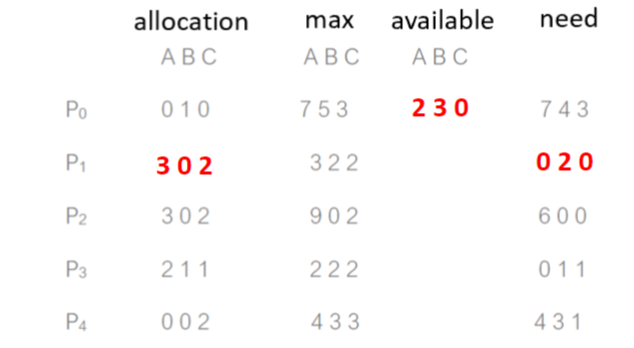
- needed[1] <= work –> work = work + allocation = [5 3 2], finish[1] = true
- needed[3] <= work –> work = work + allocation = [7 4 3], finish[3] = true
- needed[4] <= work –> work = work + allocation = [7 4 5], finish[4] = true
- needed[2] <= work –> work = work + allocation = [10 4 7], finish[2] = true
- needed[0] <= work –> work = work + allocation = [10 5 7], finish[0] = true
- P0 requests 0 2 0, still in safe state?
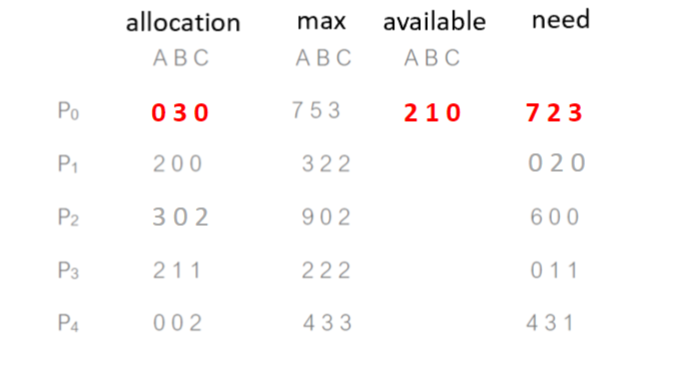
- We cannot find a process that the need[i] < work[i]
Deadlock Avoidance via Scheduling
In some scenarios deadlock avoidance is preferable.
- Global knowledge is required:
- Which locks various threads might grab during their execution.
- Subsequently schedules said threads in a way as to guarantee no deadlock can occur
- Global knowledge is required:
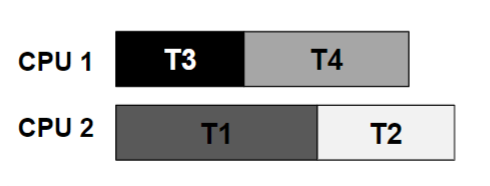
We have two processors and four threads.
- Lock acquisition demands of the threads:

- A smart scheduler could compute that as long as T1 and T2 are not run at the same time, no deadlock could ever arise.
- Lock acquisition demands of the threads:
More contention for the same resources
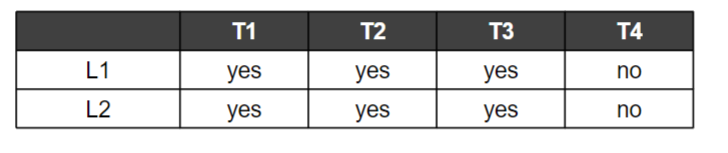
A possible schedule that guarantees that no deadlock could ever occur.
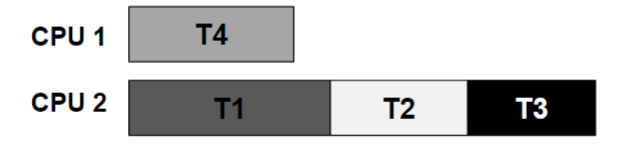
- The total time to complete the jobs is lengthened considerably.
Deadlock Detection
- System may enter deadlock state, but detect and recover from it
- Detection algorithm and recovery scheme
Deadlock Detection: Single Instance Resources
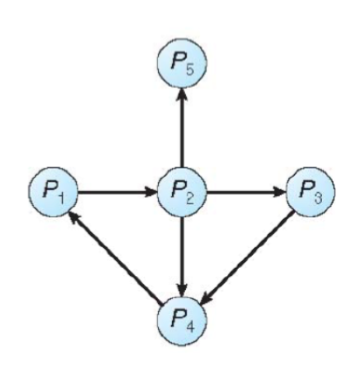
- Wait-for graph: nodes are processes
- Pi➞Pj if Pi is waiting for Pj
- Periodically searches for a cycle in the graph
- if there is a cycle, there exists a deadlock
- detecting cycles in a graph requires O(n2) operations
- n is the number of nodes in the graph
- n is the number of nodes in the graph
Deadlock Detection: Multi-instance Resources
Similar to Banker’s algorithm’s safety condition
- to prove it is impossible to enter a safe state
- Banker’s algorithm is to prove it is impossible to enter an unsafe state
- to prove it is impossible to enter a safe state
Data structures
– available: an array of length m, instances of available resource
– allocation: n × m matrix, the current resource allocated to each process
– request: n x m matrix, the current resource request of each process.
– work: an array of length m, the allocatable instances of resources
– finish: a vector of n, whether the process has been “finished”- if allocation[i] ≠0 -> finish[i] = false; otherwise, finish[i] = true
initialize:
work[j] = available[j]$\forall$j,finish[i]=falsefor all i- find process i so that
finish[i] = false && request[i,j]<= work[j];if no such i exists, go to 3 - with the above found i do
work[j] = work[j] + allocation[i,j] for all j, finish[i] = true, go to step 1 - If
finish[i] == falsethe Pi is deadlocked
- find process i so that
Key difference from Banker’s algorithm: using request[i,j] instead of
need[i,j]- Detecting whether currently is deadlocked, rather than predicting the future
Example
five processes P0 through P4
three resource types: A (7 instances), B (2 instances), and C (6 instances)

P2 requests an additional instance of type C

Deadlock Recovery
- Option 1: terminate deadlocked processes
–abort all deadlocked processes
–abort one process at a time until the deadlock cycle is eliminated
• In which order should we choose to abort? - Option 2: resource preemption
–Select a victim; rollback